検索
理化学研究所提供
（PR企画：日経サイエンス、取材/執筆：吉川和輝）
第40回（2025）京都賞（先端技術部門）を受賞する甘利俊一・理化学研究所栄誉研究員（東京大学名誉教授）。同氏の名前がメディアで取りざたされる“事件”が約1年前に起きた。10月8日、この年のノーベル物理学賞が米国のジョン・ホップフィールド氏とカナダのジェフリー・ヒントン氏に授与されると発表された。授賞理由は「人工ニューラルネットワーク（神経回路網）による機械学習を可能にする基礎的な発見と発明」。
ホップフィールド、ヒントン両氏のニューラルネットに関する業績は、2010年代後半からの「第3次人工知能（AI）ブーム」の源流と言えるものだ。物理学賞に続き9日発表のノーベル化学賞でも、タンパク質の構造を予測するプログラムの開発など、AI関連の業績が選ばれた。
物理学賞の発表直後、日本の研究コミュニティーには「なぜ受賞者に甘利先生の名前がないのか」「ノーベル賞は3人まで受賞できるのに残念だ」といった声が広がった。ホップフィールド、ヒントンの両氏と甘利氏の業績には共通点が多く、こうした驚きや惜しむ声が上がったのはもっともなことだった。
【甘利博士が登壇！京都賞記念講演会〈2025.11.11〉へのお申し込みはこちら】
ホップフィールド氏の業績は、1982年に提案したニューラルネットのモデルによって「連想記憶」と呼ばれる脳の情報処理メカニズムを定式化したこと。連想記憶は、部分的な情報から関連する記憶や概念を呼び起こす仕組みだ。例えば、ある建物の特徴的な窓の形を見ただけで外観全体を思い出したり、特定の香りを嗅いだ瞬間に過去に訪れた場所を鮮明に記憶から蘇らせたりするような脳の働きがこれにあたる。
このモデルでは、神経細胞に相当する人工ニューロンが相互に結合しており、その結合の強さ（重み）を適切に設定することで、ネットワークはエネルギーの低い安定状態へと自然に収束する。こうして記憶が再現される仕組みを示したが、このモデルと数学的に等価なモデルを甘利氏は1972年に発表している。東京大学工学部計数工学科助教授時代の業績で「甘利・ホップフィールドモデル」と呼ばれることもある。
2024年10月29日、東京大学で開いた東大・帝京大・理化学研究所による脳神経アライアンス設立シンポジウムの懇親会で。
左からヘンシュ貴雄東京大学WPI-IRCN機構長、甘利俊一氏、合原一幸東京大学特別教授
「深層学習」を60年代に先取り
一方、ヒントン氏の業績との比較では、甘利氏の研究時期はさらに古くにさかのぼる。1963年に東大大学院博士課程を終えた甘利氏は、九州大学工学部に助教授で赴任。米国のフランク・ローゼンブラット氏が1958年に提唱したニューラルネット「パーセプトロン」に強い関心を持ち、研究を進めた。パーセプトロンは、ローゼンブラット氏が提案した基本形では 入力層、中間層、出力層の3層からなる。入力信号は入力層から中間層を経て出力層に伝わり、出力層で重みづけと多数決を行い、文字や図形のパターンをカテゴリー分類する。
ローゼンブラット氏のモデルでは出力層のみが学習を担っていたが、甘利氏はニューロンが連続値を出力するよう拡張し、中間層も含めた多層ネットワークを学習できる数学的枠組みを構築した。そのために導入したのが、確率的勾配降下法という逐次学習の仕組みだ。誤差関数を定義し、その勾配に基づいて重みを1つの訓練サンプルごとに更新する方式は、局所解に陥りにくく、計算効率も高い。
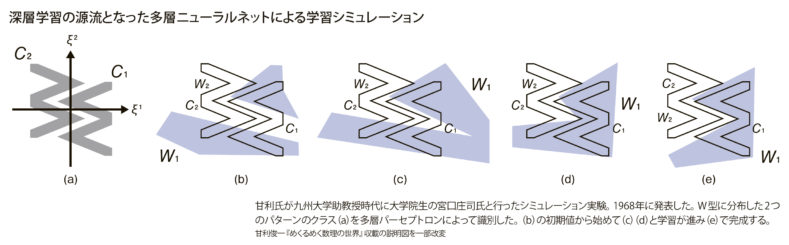
甘利氏は九大から東大へ移った1967年にこの手法を論文発表した。同時期、当時登場したばかりの国産トランジスタ計算機を使って、多層ニューラルネットによる非線形パターン識別の実験にも成功している。これは、後にディープラーニング（深層学習）と呼ばれる研究分野の先駆けとなるものだった。
ヒントン氏の代表的な業績のひとつである深層学習における「誤差逆伝播法（バックプロパゲーション）」は、20年近く下った1986年に発表されている。誤差逆伝播法は、多層ネットワークの全ての重みを勾配情報で更新する方法で、その勾配情報が確率的勾配降下法によって利用されるという関係にある。
また、深層学習の代表的なモデルで画像認識などに使われる畳み込みニューラルネットワーク（CNN）は、1979年に福島邦彦氏（現電気通信大学特別栄誉教授）が提案した階層型ニューラルネット「ネオコグニトロン」に源流を持つ。福島氏のモデルは当初教師なし学習を採用していたが、後年、ヤン・ルカン氏らが誤差逆伝播法を導入して現代のCNNに発展させた。甘利氏は、CNNはネオコグニトロンに自身の確率的勾配降下法を組み合わせて大幅に拡張されたものだと説明している。
数理脳科学の分野を確立
若き日の甘利氏が開拓した一連の学問領域は、その後「数理脳科学」と呼ばれるようになった。甘利氏は東大工学部計数工学科の教授だった1994年に理化学研究所の国際フロンティア研究システム情報処理研究グループディレクターに就任。2003年からは理研脳科学総合研究センターのセンター長を務めた。数理脳科学について甘利氏は「私が理研に設けた研究室でつけた名前である」と説明している。
数理脳科学は、数学や数理モデルの手法を使い、脳の情報処理の基本原理を解き明かすことを目指すものだ。例えば天文学の歴史では、天体の運動を観測して記述するだけでなく、その背後にある運動方程式などの物理法則が導き出された。それにより、まだ観測していない天体の動きまで予測できるようになった。
数理脳科学も同じで、脳がどのように情報を処理しているかという現象の背後にある原理を探し出そうとする。この原理を理解すれば、脳と全く同じ構造でなくても、脳の仕組みをヒントにした工学的なシステムをAIとして実現することが可能になる。
甘利氏の研究はニューラルネット研究を理論的に支える基盤となり、やがて深層学習AIによる大規模言語モデル（LLM）などへと発展した。AIの社会実装が今猛烈な勢いで進んでいるのは、甘利氏が数十年前にまいた理論研究という種が、豊かな実を結び始めている証でもある。
情報幾何学を体系化
数理脳科学と並び、甘利氏が独自に切り開いてきた学術分野が情報幾何学だ。甘利氏がこの分野の研究に本格的に乗り出したのは、九大から東大に移って10年ほどを経た1978年ころのことだった。当時の思いを甘利氏は次のようにつづっている。
「好きな研究を自由にやらせる」甘利流の指導は多くの人材を引き付けた
「私は神経回路網の数理を10年夢中で研究し、『神経回路網の数理』なる著書を書き終え、少し飽きが来ていたのだろうか。この分野の専門家になったと感じたが、専門家とは職人でもある。（略）でも、職人としての専門家では満足できない。数理工学を考究する自分の可能性はもっと他にもあるのではないだろうか。長年の夢でもあった統計の微分幾何学に新しい可能性を見出せるかもしれない」（『めくるめく数理の世界』から）
「長年の夢でもあった」というのは、甘利氏は東大大学院数物系研究科の修士課程で履修した森口繁一教授による統計学のセミナーで、後の情報幾何学につながる統計学の手法に触れ、その方法の「美しさ」に魅せられたという経験があったためだ。
情報幾何学の典型的な手法は、統計モデルなど確率分布の集まりを多様体（曲がった幾何学空間）として捉え、確率分布間の類似度や違いを測地距離（幾何学的な距離）や曲率（曲がり）として定量化し、その構造を分析する数学的な枠組みだ。
ここでは、統計モデルのパラメーターをデータからどれだけ正確に推定できるかを示す尺度であるフィッシャー情報量を使い、リーマン計量と呼ばれる多様体上の「物差し」を与えてその幾何学的性質を明らかにする。
森口教授の統計学セミナーでは、こうしたリーマン計量やフィッシャー情報量を統計学に応用するという当時最先端のアイデアが紹介された。統計と幾何学を融合させる発想に初めて出会った甘利氏は強い刺激を受けた。それから20年近くを経て、数理脳科学の研究と並行して情報幾何学の体系化に取り組むことになる。
統計分野に微分幾何学を応用した甘利氏の論文が、統計の一流誌Journal of Mathematical Statisticsに掲載されたのは1982年。その後来日した統計学の第一人者である英国のコックス卿が甘利氏から説明を聞き、これが甘利氏を招いてのロンドンでのワークショップ開催につながる。統計の微分幾何というコンセプトは甘利氏が名付けた「情報幾何学」として世界に広がっていった。
甘利氏は情報幾何学の体系化を進める一方、その研究手法を数理脳科学の研究にも自ら応用して成果を上げてきた。代表的な成果は1990年代に提案した、機械学習や統計モデル向けに使われる「自然勾配法」という最適化手法だ。
通常の勾配降下法は、パラメーター空間をユークリッド空間（平らな空間）と仮定し、その座標系での勾配方向に沿ってパラメーターを更新する。しかし実際の確率モデルのパラメーター空間は「曲がっている」ことが多い。自然勾配法ではこの空間の曲がりを考慮して、効率よく最適化作業を進めることができる。屈折率は別の観点から求めることもできる。光は電場と磁場が物質と相互作用しながら伝わっていく波だ。電場に関する誘電率（ε）、磁場に関する透磁率（µ）という2つのパラメーターが強く関係する。誘電率が大きいほど、物質は電荷を多く蓄えることができ、透磁率が高いほど、磁場を通しやすくなる。屈折率はこの2つのパラメーターの平方根の掛け算で計算される（n ＝√ε×√µ）。
多彩な研究者を輩出
甘利氏の独創的な研究活動は、多くの研究者を引き付けた。カオスニューラルネットワークの研究で知られる合原一幸東京大学特別教授もその1人。1982年に東京大学大学院の博士課程を終えた合原氏は大学教員としてのポストも決まっていたが「どうしても甘利先生の下で学びたくなり」、内定を辞退してポストドクターとして1年間指導を受けた。
合原氏は大学院では電子技術総合研究所（現産業技術総合研究所）の松本元氏の下でヤリイカの神経を使った研究で神経のカオス現象を発見した。これは単一のニューロンにおける発見だったが、「これがニューロンのネットワークでどのような現象を生みだすか、甘利先生の数理の手法を使いたいと思った」という。合原氏は後に東京大学で甘利氏とコンビで研究室を運営することになる。
合原氏によると「海外では日本にアマリという研究者が2人いると誤解している研究者が少なくない」という。数理脳科学と情報幾何学という2つの分野であげた甘利氏の膨大な業績をみて、1人の人間でできるはずがないと思うのだろうという。「数理脳科学と情報幾何学は、甘利先生の頭の中では別々のものではなく、繋がっていたのだと思う」と語る。
理化学研究所提供
2017年3月16日、甘利氏の理化学研究所の研究室をクローズするのに合わせ理研でワークショップ「Mathematical views in neuroscience and AI」が開かれた。
自由の空気に満ちた研究室
甘利氏が2024年10月に出版した著書に収録された英語論文のリストには1962年から2024年10月までの62年間で329件のタイトルがある。「甘利先生は飛行機に乗るたびに新しい論文のアイデアが浮かぶと言っていた」というのは、理研脳神経科学研究センター（理研CBS）数理脳科学研究チームでチームディレクターを務める豊泉太郎氏だ。
豊泉氏は学生時代に情報幾何学に関心を持ち、大学院は東大の合原研究室に進んだ。博士課程の最後の年と、渡米後に理研の甘利氏の研究室で研究生活を送った。「研究室は自由な空気が満ちており、若手の研究者の自主性を尊重してくれるリーダーだった」という。名物行事は甘利氏の自宅で毎年開かれるホームパーティー。「国内外の高名な研究者もよく顔を出し、あちらこちらで談笑の輪ができていた」と振り返る。
甘利氏が開拓した数理脳科学と情報幾何学という2つの学術領域は、相互に関係しながら発展を続けている。AIに情報幾何学の手法で磨きがかけられると同時に、情報幾何学の応用先はAIに限らず、量子情報や情報通信技術、さらには経済学など社会科学の領域にも広がろうとしている。甘利氏が幅広い学術領域で営々と築き上げてきた業績が、未来の科学技術の革新に計り知れない影響を与え続けることは間違いないだろう。
〈本記事は日経サイエンス2025年11月号（9月25日発売）に掲載されました。〉